回顾线性代数

图形学所依赖基础

源：GAMES101_Lecture_02 (ucsb.edu)

• 基础数学
  • 线性代数
  • 微积分
  • 统计学
• 基础物理学
  • 光学
  • 机械原理
• 工程学
  • 信息处理
  • 数据分析

向量（Vectors）

• 笛卡尔坐标系
  • X和Y分量能被正交分解成任意单位向量$$ A=\dbinom{x}{y}$$$$\mathbf{A}^\mathrm{T} = (x, y)$$ $$||A||=\sqrt{x^2+y2}$$
• 向量的表示
• 一般写成箭头或粗体 $$\vec{a} 或 \boldsymbol{a}$$
  • 也可以使用两点进行表达（终点减起点）$$ \vec{AB} = B-A $$
  • 可通过向量知道方向以及长度
  • 无需绝对的起点(原因？)
• 向量模长的表示 $$ ||\vec{a}||$$
• 单位向量
  • 向量的长度为1的向量称之为单位向量
  • 可求得某个一个向量的单位向量（归一化）$$\hat{a} = \vec{a} / ||\vec{a}||$$
  • 常用来表示向量的方向

向量加法（Vector Addition）

• 几何表示：四边形法则 / 三角形法则
• 代数表示：简单的对应坐标相加

向量的几何分解

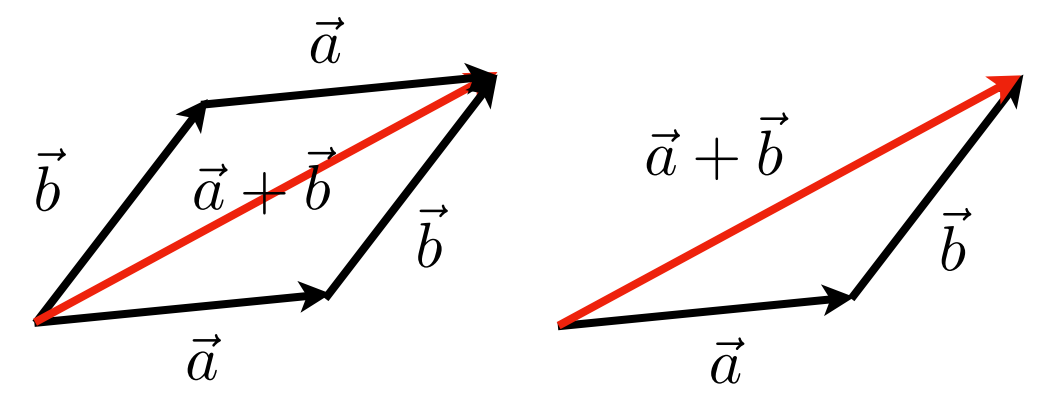
向量乘法（Vector Multiplication）

向量点乘（dot product）-> 数量积，标量

计算原理

一般向量的计算：$$\vec{a}·\vec{b}=||a||·||b||·\cos{\theta}$$

$$\cos{\theta}=\frac{\vec{a}·\vec{b}}{||a||·||b||}$$

对于单位向量而言，这对于计算向量的夹角特别有用，可以将向量归一化为单位向量，再通过点乘，就可以得到夹角的余弦值：$$\cos{\theta}=\vec{a}·\vec{b}$$

向量点乘支持的计算规则

• 交换律
• 分配律
• 结合律

向量计算的规则

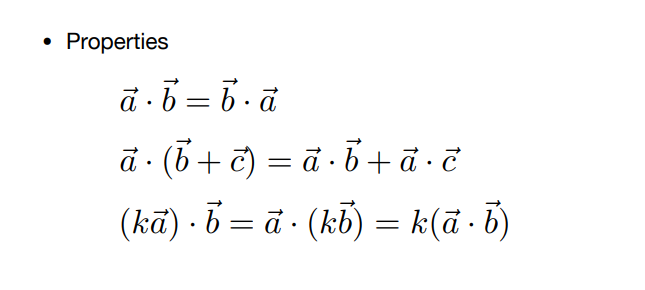
笛卡尔坐标系中的点乘

对应坐标的元素相乘，最后求和即可

笛卡尔坐标系中的点乘

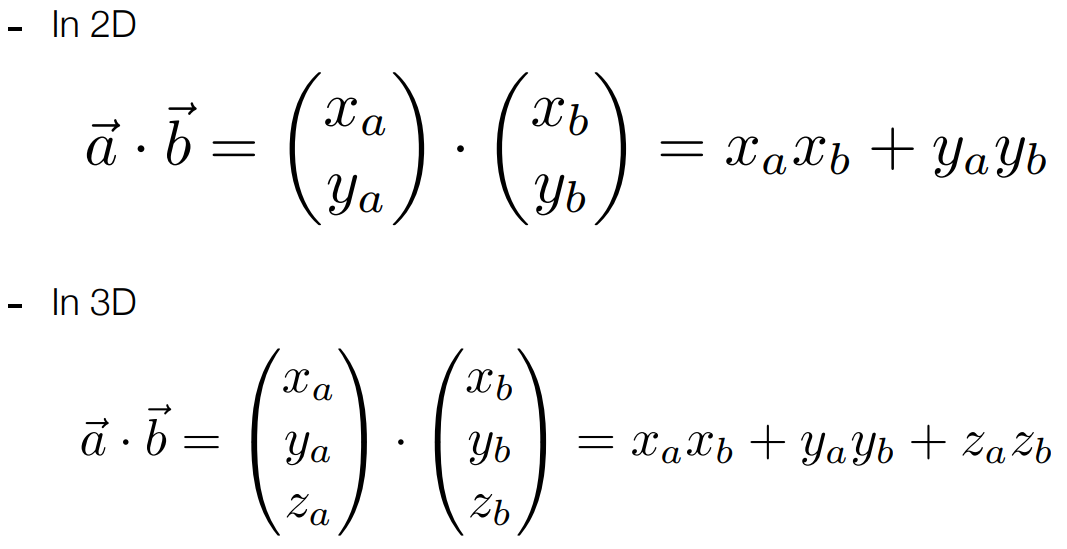
向量点乘在图形学的应用

• 计算两个向量之间的夹角、
  • eg: 点光源与物体表面的余弦值
• 计算一个向量在另一个向量上的投影
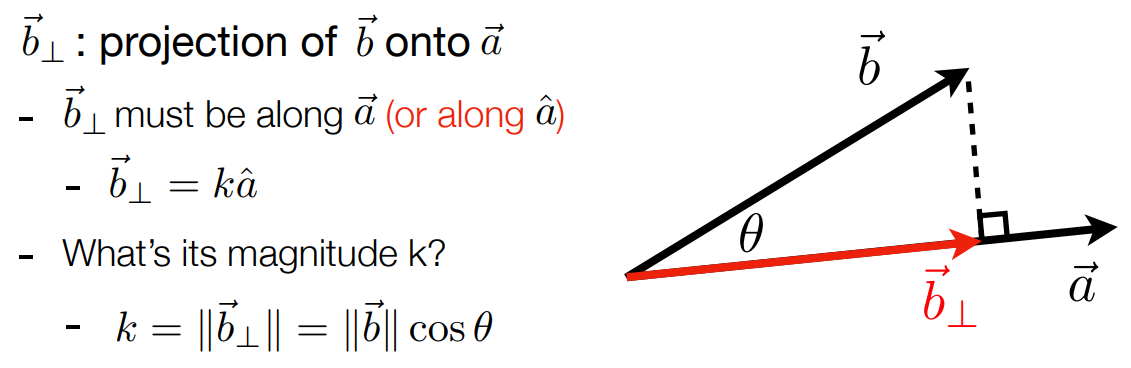
  • eg: 阴影计算
• 计算两个向量的距离
• 正交分解（分解一个向量）
• 判断位置的前和后（根据余弦的图像可知，夹角小于90度则为正，即为前面；大于90小于180则为负，即为后面）

点乘在图形学中的应用-向量前后判断

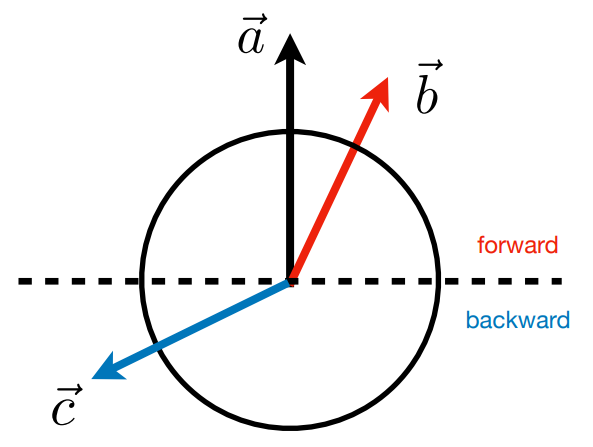
向量叉乘（cross product）-> 向量积，向量

计算原理

叉乘原理

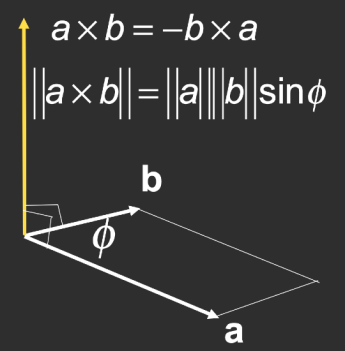
• 叉乘后的向量是两个向量的正交向量
• 叉乘向量的方向是通过右手坐标系决定的，因此，可以根据叉乘后的向量判断坐标系（左手系/右手系）
• 在笛卡尔坐标系中很有用？

向量叉乘支持的计算规则

叉乘支持的计算规则.png

矩阵（Matrices）